Explain How to Determine the End Result of a Polynomial

By Ra_Karen17 15 Apr, 2022 Post a Comment

After doing this we will find two factors of ac that will add up to give us b. In this case it is 7.

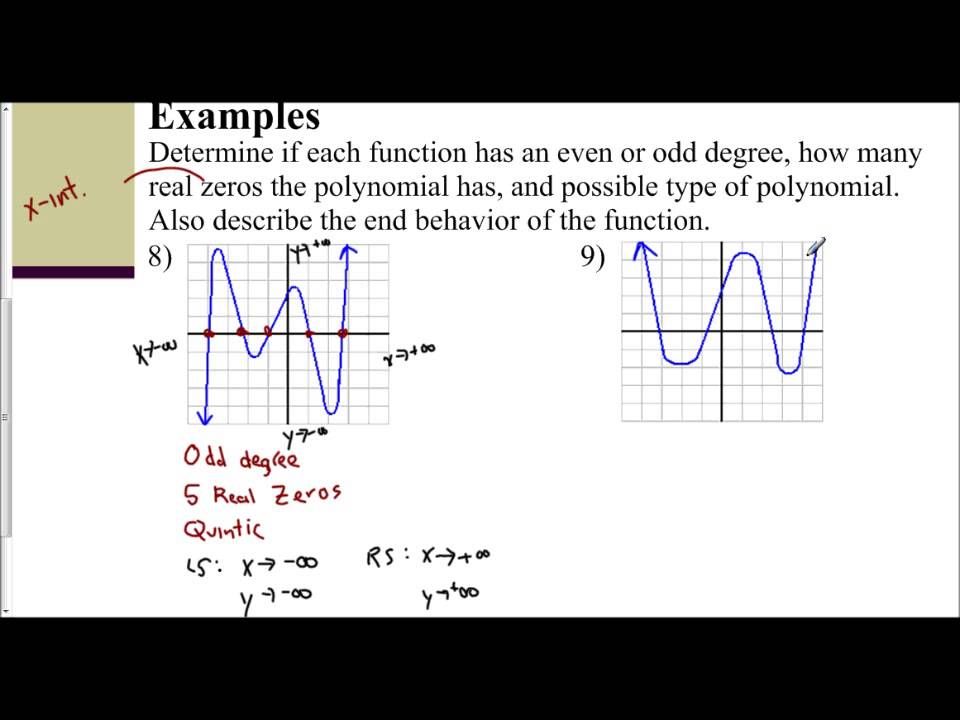
Lesson 6 3 Identifying Even Odd Degree Functions Zeros End Behavior Lesson Behavior Polynomial Functions

Q x x 3 6x 3x 4.

. Cubic polynomial with negative leading coefficient like y-2x33x2x1. The reduced polynomial is 4x² 6x 24. Now you must solve.

Notice that as you move to the right on the -axis the graph of goes up. When we write f x g x Q x R x g x it highlights the fact that we can find both the quotient and the remainder functions by dividing f x by g x. The leading coefficient test is a quick and easy way to discover the end behavior of the graph of a polynomial function by looking at the term with the biggest exponent.

The degree of a polynomial is the highest exponent of a term. Ensure that the number of turning points does not exceed one less than the degree of the polynomial. Use modulo-2 binary division to divide binary data by the key and store remainder of division.

So with our example polynomial a is 10 b is 8 and c is -9. Endcases where the options attribute is a list containing n-tuples specifying the exponent of each feature in the dataset for each term in the polynomial expansion. A fx -2x - 1x 1x - 2 B gx x - 1x 22 x - 12 View Answer.

Check if the leading coefficient is positive or negative. To do this we need to learn the method for long division of polynomials. Knowing the degree of a polynomial function is useful in helping us predict its end behavior.

The function is not a polynomial function because the term 2x -2 has an exponent that is not a whole number. Weve got the study and writing resources you need for. The degree of the polynomial is the highest degree of any of the terms.

Quartic polynomial with positive leading coefficient like y5x43x24x9. Up to 10 cash back Give the degree of the polynomial. The polynomials are the expression written in the form of.

Find the Degree of this Polynomial. Determine the end behavior by examining the leading term. 2 on a question.

In other words 4x³ 15x 36 x32 4x² 6x 24. To determine its end behavior look at the leading term of the polynomial function. If it is even then the end behavior is the same ont he left and right if it is odd then the end behavior flips.

End behavior is another way of saying whether the graph ascends or descends in either direction. Explain how to determine the long term end behavior of the following two polynomials. 5x 14y - 2z -36 7x 3y 4z 22 3x - 2y - Z 9.

Px 3 x² 2x 4 is of this type because it does not lack any exponent between 2 and 0. Thus the degree of the polynomial will be 5. First week only 499.

Start your trial now. Therefore lets find the product of 10 and -9. We want to find the product of the terms a and c.

Solution for Explain how to determine the leading coefficient of a polynomial. Knowing the leading coefficient and degree of a polynomial function is useful when predicting its end behavior. Append the remainder at the end of the data to form the encoded data and send the same Receiver Side Check if there are errors introduced in transmission.

The binary data is first augmented by adding k-1 zeros in the end of the data. To determine its end behavior look at the leading term of the polynomial function. If positive then it is increasing to the right if it is negative then end behavior decreases to the right.

4x² 6x 24 0. First divide out the common factor of 2. 2x² 3x 12 0.

A n x n a n-1 x n-1 a 1 xa 0. The exponents of the terms of this polynomial are in order 5 4 2 and 7. In other words the end behavior of a function describes the trend of the graph if we look to the right end of the -axis as approaches and to the left end of the -axis as approaches.

We then try to factor each of the terms we found in the first step. ℎ 7 712 56 32 18 c. Use the end behavior and the behavior at the intercepts to sketch a graph.

Find the sum of 3sqrt 2 and 2sqrt 8 in simplest form. For example consider this graph of the polynomial function. 5x 5 7x 3 2x 5 9x 2 37x4.

Method for Dividing Polynomials. The degree of an individual term of a polynomial is the exponent of its variable. For example the following expression.

Describe the end behavior of the graph of the functions given below. Determine zeros degree of the polynomial and the leading term of each of the polynomial and sketch the graph. When we find a polynomial that has monomials with all possible exponents from the highest degree to the independent term we say that it is a complete polynomial.

The formula for the root of linear polynomial such as ax b is. To find the degree of the given polynomial combine the like terms first and then arrange it in ascending order of its power. For each graph determine whether it represents an odd or even-degree polynomial and determine the sign of the leading coefficient positive or negative.

The reduced polynomial has degree 2 so there is no need for more trial and error and you continue to step 5. We can now make use of the exponents stored in the options attribute in order to calculate the actual terms in the polynomial expansion. This continues until we simply cant factor anymore.

12 223 12 2 2 3 Factoring polynomials is done in pretty much the same manner. Using ac we will list all available factors. 32 is a root.

Also determine whether the result is rational or irrational and explain your answer. So 5x 5 7x 3 2x 5 9x 2 37x4 7x 5 7x 3 9x 2 7x 7. 5 47 36 29 2 b.

Because the power of the leading term is the highest that term will grow significantly faster than the other terms as x gets very large or very small so its behavior will dominate the graph. Ax 2 bx c 0. Because the power of the leading term is the highest that term will grow significantly faster than the other terms as x gets very large or very small so its behavior will dominate the graph.

Use the multiplicities of the zeros to determine the behavior of the polynomial at the intercepts. The standard form of a polynomials has the exponents of the terms arranged in descending order. 2 412 81715 2.

We determine all the terms that were multiplied together to get the given polynomial. The general form of a quadratic polynomial is ax 2 bx c and if we equate this expression to zero we get a quadratic equation ie. The Coefficient of the Leading Term Determines Behavior to the Right.

What Is A Quadratic Polynomial Explained With 10 Examples Quadratics Polynomials Math Methods